This project is a reactive web app that simulates a variety of common epidemiological models. Epidemics can be modelled mathematically in order to make forecasts and, if necessary, take countermeasures in time. 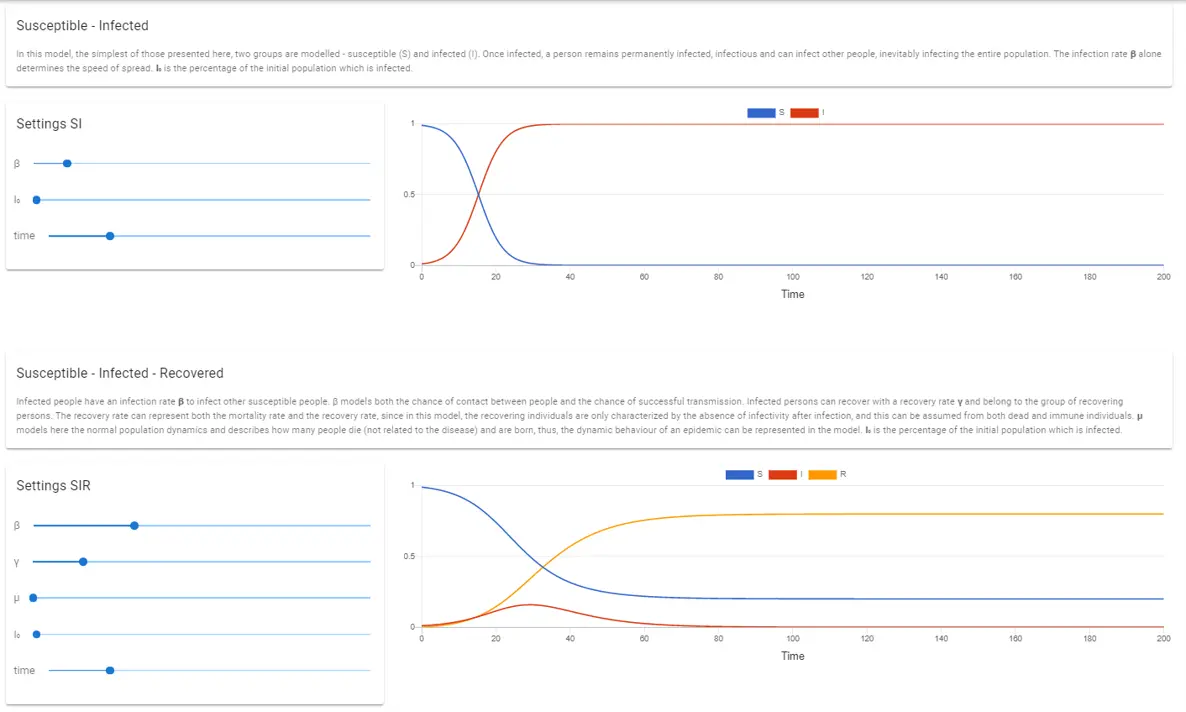The most known epidemiological model was developed in 1927 by William Ogilvy Kermack & Anderson Gray McKendrick, which divides the population into three groups: susceptible (S), infected (I) and recovered (R) and also models the interactions between them. Infected people have an infection rate β to infect other susceptible people. β models both the chance of contact between people and the chance of successful transmission. Infected persons can recover with a recovery rate γ and belong to the group of recovered persons. The recovery rate can represent both the mortality rate and the recovery rate, since in this model, the recovering individuals are only characterized by the absence of infectivity after infection, and this can be assumed from both dead and immune individuals. μ models here the normal population dynamics and describes how many people die (not related to the disease) and are born, thus, the dynamic behavior of an epidemic can be represented in the model. I₀ is the percentage of the initial population which is infected.

Besides this probably best-known model, there are other mathematical models available. This web app is mainly intended as a learning tool to get a feeling for epidemiological models.